https://www.acmicpc.net/problem/14578
14578번: 영훈이의 색칠공부
영훈이가 색칠 할 수 있는 모든 경우의 수를 1,000,000,007로 나눈 나머지를 출력하시오.
www.acmicpc.net
문제 요약 : nxn 격자가 있다. 각 행과 열에 빨간색과 파란색이 하나씩 색칠되어야 한다. 모든 경우의 수는?

예제 입력1
3
예제 출력1
12
시도 )
처음에 문제를 잘못알아들어서
흰색칸이 생길 수 있는 경우의 수만 찾았다(ㅋㅋ).. 왜 틀렸지 하고 붙잡고 있었음
그런데 그덕분에 풀이에 좀 가까워진 것 같기도..?!
참고로 아예 틀린 풀이다.
# 영훈이의 색칠공부
N = int(input())
dp = [0,0,0,12]
if N > 3 :
for i in range(4,N+1):
dp.append(dp[i-1]*i)
print(dp[N]%1000000007)
else :
print(dp[N])
📌 풀이 )
이 문제는 교란순열을 사용한 문제이다.
사실 도저히 모르겠어서 질문게시판을 참고했다가, 교란 순열이라는것이 있는 것을 알게되어 겨우 풀었다..
교란순열은 차후 포스팅하도록 하겠다.
일단 첫번째 색상을 칠할때에는, N!이 된다.(일단 파란색이라고 가정함)
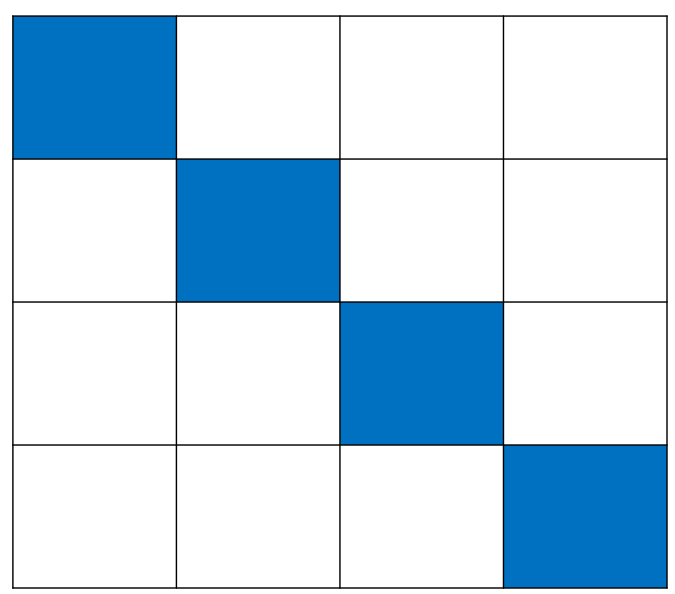
다음 두번째 색상이 문제이다.(빨간색이라고 가정함)
이 파트가 교란 순열이 들어간 부분인데, 쉽게 말하면 자신의 시험지를 매기지 않는 경우를 찾는 방법이다.
N개의 색상을 파란색 칸을 제외하고 고르는 것을 D(n)이라고 가정하자. (즉, 자신의 시험지를 제외하고 고르는 경우)
- 일단 첫번째 칸에서는 파란색으로 칠해진 부분을 제외하고 골라야하므로 (N-1)개 고를 수 있다.

- 두 번째 칸은 두가지로 나누어진다.
- 첫번째 선택과 교차하여 선택하였을 때 : 즉 첫번째 선택의 칸을 고르는 경우이다.
=> 그러면 2가지 색상을 제외하고 다시 n-2개의 색상이 서로 교차되지 않게 골라야하므로 D(n-2)가 된다.
- 첫번째 선택과 교차하여 선택하였을 때 : 즉 첫번째 선택의 칸을 고르는 경우이다.

- 첫번째 선택과 두번째 선택 모두 해당하지 않을 때
=> n-1개의 색상이 서로교차되지 않게 골라야하므로(이때 첫번째 색상과 두번째 색상을 바꾸어 생각하면 된다.) D(n-1)개가 된다.

여기서 "이때 첫번째 색상과 두번째 색상을 바꾸어 생각하면 된다." 이 말이 헷갈릴 수 있는데,

D(n-1)을 통해 이렇게 나온다 가정하면,
2번째 줄에 칠해진 값들은 무조건 첫번째 칸에 칠해진다고 생각하면 됨.

그러면
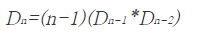
(n > 2)
이러한 식이 만들어진다.
첫번째 색상에 두번째 색상의 경우를 곱하면
N! * Dn이 되므로 아래와 같이 계산할 수 있다.
# 영훈이의 색칠공부
N = int(input())
dp = [0,0,1]
fact = 2
mod = 1000000007
if N > 2 :
for i in range(3,N+1):
dp.append(((dp[i-1]+dp[i-2])*(i-1))%mod)
fact *= i
print((fact*dp[N])%mod)
else :
if N == 1:
print(0)
else :
print(2)
'코테 공부 🔥' 카테고리의 다른 글
| [프로그래머스/파이썬] 이모티콘 할인행사 (1) | 2023.05.13 |
|---|---|
| [백준/파이썬] 16724: 피리 부는 사나이 (0) | 2023.05.01 |
| [백준/파이썬] 1043: 거짓말 (0) | 2023.05.01 |
| [백준/파이썬] 14719: 빗물 (0) | 2023.04.20 |
| [프로그래머스/SQL] 입양 시각 구하기(2) (0) | 2023.04.20 |




댓글